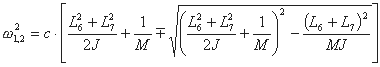Example: eigenfrequency computation
This example shows how to determine the Eigenfrequencies of a sewing machine.
We assume that you are familiar with the topic, but want to know
how to solve the mathematical side with MasterAllRound.
Here is a short version of an example from the manual showing some additional options in
MasterAllRound:
You obtain the Eigenfrequencies by solving the following equation:
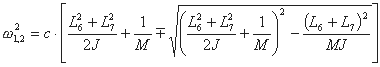
with c defined as:
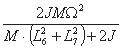
Input data are:
- L6 = 220 mm
- L7 = 120 mm
- M = 18 kg (mass of the machine)
- J = 0.18 kgm2 (mass moment of inertia)
- n = 1000 min-1 (nominal speed)
Units are [N], [mm] and [s].
First, we enter the above constants. Note that you can add comments when
defining constants in MasterAllRound:
- L6 = 220 ' [ mm]
- L7 = 120 ' [ mm]
- M = 18/1000 ' [N*s^2/mm]
- J = 0.18E3 ' [N*mm*s^2]
- OMI = 2*PI*1000/60 ' n = 1000 min^(-1)
We rewrite the equation using sub-equations:
- TC = 2*J*M*OMI^2/(M*(l6^2+L7^2)+2J)
- TG1 = (L6^2+L7^2)/(2J) + 1/M
- TG2 = (L6+L7)^2/(M*J)
That's all on the set-up side: we can solve the task by entering in
the formula input field our equation:
- f1 = (SQR(TC*(TG1-SQR(TG1^2-TG2))))/(2*PI) ' @
The "@" indicates that we are using sub-equations.
Finalizing our input with the return key, or clicking on the "Run!" button, gives us the result:
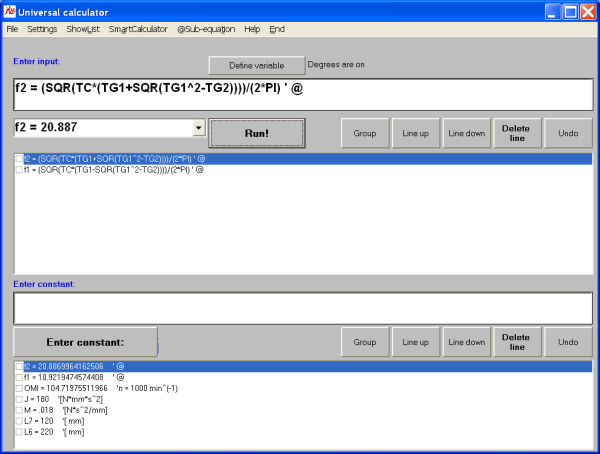
To obtain the second solution, we just edit the equation in the input field:
- "f1" in "f2"
- "-SQR" in "+SQR"
The second equation is:
- f2 = (SQR(TC*(TG1+SQR(TG1^2-TG2))))/(2*PI) ' @
We finalize our input with the return key and obtain the second frequency:
It's very easy to investigate changes in the Eigenfrequencies now. For example: all we have to do,
to study how f1 changes as a function of M, is to define M as a variable. As a result, we obtain
ordered pairs of M and f1. We can also plot this by saving the table and using the plot module of MasterAllRound.
(To basic example)
(To example fracture mechanics computation)
(To MAR Cal)
(To MAR Plus)
|