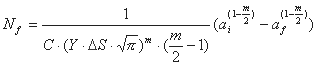MasterAllRound: der PC-Rechner

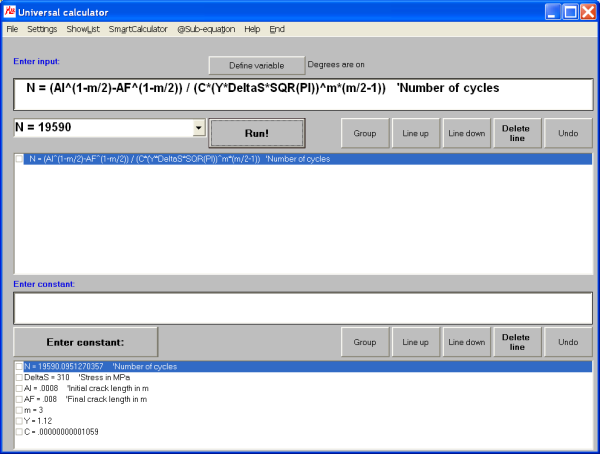
Example: crack growth (fracture mechanics)

This example explains how to solve a problem from linear fracture mechanics with MasterAllRound. The equation includes exponents.

In linear fracture mechanics, the crack growth can be solved by integrating the Paris law:

with

where K is the stress intensity factor and Y the compliance function, describing the geometry of the structure in which the crack exists. For some cases, Y is constant and independent of the crack length. Using this assumption is also a quick way to assess the performance of a structure. For a constant Y, the integration for m ≠ 2 is straightforward and leads to:
Solution of the integral

Given the following input data:

Stress range ΔS in [MPa]: 310
Initial crack size a_i in [m]: 0.8E-3
Final crack size a_f in [m]: 8E-3
C = 1.059E-11 [m/Zyklen]
Y = 1.12
m = 3

The input and result (N = 19590) in MasterAllRound are:

(To basic example) (To example eigenfrequency computation) (To MAR Cal) (To MAR Plus)